Electric vehicles (EVs) are one of the most promising technologies to reduce greenhouse emissions in logistics and transportation systems. However, they suffer from a number of technical constraints to which their combustion engine-powered counterparts are immune (e.g., long charging times, limited autonomy). As it stands, incorporating EVs into logistics operations presents new challenges for the vehicle routing community. Since they began to appear on the consumer market about 10 years ago, the interest in EV routing problems (E-VRPs) has been constantly increasing. Nonetheless, the richest E-VRP variants are still open. This Challenge will consider two related variants:
- E-VRP with nonlinear charging function (E-VRP-NL) and
- E-VRP-NL with capacitated charging stations (E-VRP-NL-C).
E-VRP-NL Problem Statement
The E-VRPNL was introduced by Montoya et al. (2017). The problem can be formally defined as follows. Let I be a set set of customers that need to be served and F be the set of charging stations (CSs) at which vehicles may stop to recharge their battery. Each customer i ∈ I has a service time gi. The customers are served using a homogeneous fleet of EVs. Each EV has a battery of capacity Q (expressed in kWh).
At the beginning of the planning horizon, the EVs are located in a single depot, from which they leave fully charged. The depot is continuously open for Tmax hours. Traveling from one location i (the depot, a customer, or a CS) to another location j incurs a driving time tij ≥ 0 and an energy consumption eij ≥ 0. Driving times and energy consumption both satisfy the triangle inequality. Due to their limited battery capacity, EVs may have to stop en route at CSs. Charging operations can occur at any CS, they are non-preemptive, and EVs can be partially recharged.
Each CS j ∈ F has a piecewise linear concave charging function φj(Δ) that maps, for an empty battery, the time Δ spent charging at j to the state of charge (SoC) of the vehicle upon departing from j. For instance, if q is the SoC of the EV upon arrival at j and Δ is the charging time, the SoC of the EV upon departure from j is given by φj(Δ+φj-1(q)). The figure below illustrates the charging process.
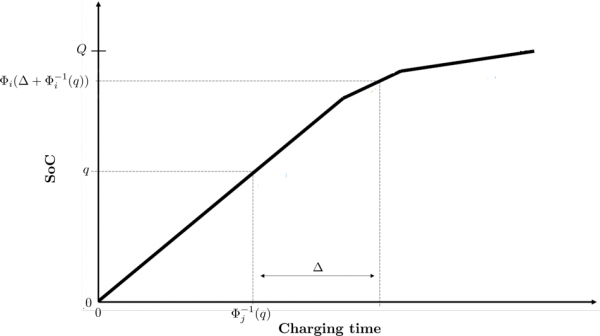
Feasible solutions to the E-VRP-NL must satisfy the following conditions:
- each customer is visited exactly once by a single vehicle;
- each route starts at the depot not before time 0 and ends at the depot before time Tmax; and
- each route is energy-feasible (i.e., the SoC of an EV when it arrives at and departs from any location is between 0 and Q).
The objective of the E-VRP-NL is to minimize the total time needed to serve all customers, including driving, service, and charging time. In this variant of the problem, CSs are assumed to have an infinite capacity, meaning that there is no limit on the number of EVs that can be charged simultaneously at any station and, therefore, never any waiting time at a CS.
More detailed definitions of the problem and multiple mixed linear integer programming models formalizing it can be found in Montoya et al. (2017) and Froger et al. (2019).
E-VRP-NL-C Problem Statement
The E-VRP-NL-C variant was introduced by Froger et al. (2021). The problem follows the exact same definitions given above for the E-VRP-NL with the notable difference that CSs have a limited capacity in E-VRP-NL-C.
More specifically, in the E-VRP-NL-C, each CS j ∈ F has a capacity, given by the number Cj of available chargers, which restricts the number of EVs that can be simultaneously charged. Due to the limited capacity of CSs, waiting times may occur at CSs whenever an EV queues for a charger. In addition to the three feasibility conditions enumerated for the E-VRP-NL, feasible solutions for the E-VRP-NL-C must also satisfy a fourth condition:
- no more than Cj EVs can simultaneously charge at each CS j ∈ F.
Similar to the E-VRP-NL, the objective is to minimize the total time needed to serve all customers, including driving, service, charging and waiting time. Note that to avoid congestion at CSs starting times of the routes may be delayed at no cost.
A more detailed description of the problem and a set of mixed integer programming formulations formalizing it can be found in Froger et al. (2021).
Electric VRP Instances
E-VRP-NL: The E-VRP-NL competition will use instances introduced in Montoya et al. (2017). The set includes 120 instances ranging from 10 to 320 customers. A full description of the instance set can be found in Section 4.1 in Montoya et al. (2017). The best known solutions for this set were reported in Froger et al. (2021). The instances are available at VRP-REP.org (VRP-REP-ID 2016-0020). [Download E-VRP-NL instances]
E-VRP-NL-C: The E-VRP-NL-C competition will use instances introduced in Froger et al. (2021) by adding CS capacity constraints to the Montoya et al. (2017) set. From each of the original 120 instances, two new instances are obtained by setting the number of available chargers on each of the CSs to 1 and 2, respectively. The best known solutions for the resulting 240 instances are reported in Froger et al. (2021).
Electric VRP Algorithm Evaluation
Solvers will be evaluated primarily based on solution quality. Each competitor must submit a single zipped file containing one solution file per instance. The solution files must be xml files complying with the xml schema specified in the dimacs-evrp-solution.xsd file. You can find here an example output file reporting the solution delivered by the mixed integer programming model of Montoya et al. (2017) for instance tc2c10s2cf0. You can use the online validator from FREEFORMATTER.com (available here) to check that your solver is producing valid output files. If you are competing only in the E-VRP-NL category, your submission package is expected to contain 120 files. If you are competing only in the E-VRP-NL-C category, your submission package should contain 240 files. If you are competing in both categories, 360 files are expected.
Output File Names:
- Solution files for the E-VRP-NL variant should simply be named using the ID of the corresponding instance. For example, the solution file for the E-VRP-NL version of the tc2c10s2cf0 instance should be named tc2c10s2cf0.xml.
- Solution files for the E-VRP-NL-C should be named using the ID of the instance with the “-C#” suffix (where # is the number of available chargers). For example, the solution for the E-VRP-NL-C version of the tc2c10s2cf0 instance with 1 charger per charging station should be named tc2c10s2cf0-C1.xml. Similarly, the solution for the version of the instance with 2 chargers per charging station should be named tc2c10s2cf0-C2.xml.
Solution Checker
A solution checker is available on github. Instructions for its use are contained in the associated readme file. We thank Nicolas Cabrera for his assistance in implementing it.
Solver Scoring
Points will be awarded to your solver as follows.
First, for each instance:
- +5 points for each exclusive new best-known solution (BKS) that is also optimal.
- +3 points for each exclusive new BKS.
- +2 points for each non-exclusive optimal BKS.
- +1 point for each non-exclusive BKS.
- -3 points for each infeasible solution.
- -3 points for each missing or invalid solution file.
We note that no points are awarded for a feasible solution that is not as good as the solution of [FJML21] (but no points are deducted either!).
And then overall:
- +10 points if your gap with respect to the BKS for every instance is lower than or equal to 1%.
- +10 points if your average gap with respect to the BKS across all instances is the lowest among all competing solvers.
- +10 points if your solver is the fastest (i.e., the total time invested to solve all the instances is the lowest among all competing solvers) AND its average gap with respect to the BKSs across all instances is less than or equal to 5%.
Please note that by the BKS of an instance we mean the best solution reported either by Froger et al. (2021) or by any competing solver. In other words, the BKS for each instance is fixed after checking and validating the solution files submitted by all the competitors for that instance. Note also that, by new exclusive BKS we mean a BKS that only your solver unveiled.
Please note that the CPU times will not be scaled to account for programming languages or machine configurations.
Finally, it is worth mentioning that the organizers do not have a practical way to verify the optimality of the solutions you report, therefore that part of the score is based on the honor system. That said, the organizers may ask you to submit proof of optimality (e.g., CPLEX logs) for some or all your solutions to validate your points.
The winner for each category is the solver scoring the most total points across all instances.
Submission
When you are ready to submit either your solver output package (a zipped file) or your Challenge paper, you may do so from the Submissions page (which is part of the navigation menu on the right-hand side of this page).
Outputs are due January 30, 2022 and must be received by 23:59 Pacific Standard Time (UTC -8).
Electric VRP Organizer(s)
Jorge Mendoza (lead)
Nicholas Kullman
Questions
If you have questions, please email the organizers using this link.
References
[FMJL19] A. Froger, J.E. Mendoza, O. Jabali, G. Laporte. Improved formulations and algorithmic components for the electric vehicle routing problem with nonlinear charging functions. Computers & Operations Research. 104:256-294, 2019.
[FJML21] A. Froger, O. Jabali, J.E. Mendoza, G. Laporte. The electric vehicle routing problem with capacitated charging stations. Working Paper. Available at: https://hal.archives-ouvertes.fr/hal-02386167. Last Accessed: July 13, 2021.
[MGMV17] J.A. Montoya, C. Guéret, J.E. Mendoza, J.G. Villegas. The electric vehicle routing problem with nonlinear charging function. Transportation Research Part B. 103:87-110, 2017.


